Transportation and delivery make up a significant portion of the cost of many products. As society’s demands become more complex and fast-paced, optimizing route logistics can result in huge savings for many companies. In recent years, researchers have been inspired by quantum computing to create better optimization algorithms now, and even better ones in the future as quantum technology matures.
As the demands of these services continue to expand in scale and complexity, quantum and quantum-inspired computing can be the answer to solving logistical problems more efficiently.
Route optimization is a systematic process of finding the most cost-effective, or efficient path that should be taken given a set of criteria. Two well-known examples of route optimization problems are the travelling salesperson problem (TSP), and the vehicle routing problem (VRP).
In essence, the TSP asks the question, ‘What is the shortest round-trip that one salesperson can take given a number of different destinations?’ The VRP generalizes this by asking, ‘What is the optimal set of routes that a number of vehicles should take in order to travel to a given set of destinations?’
The VRP and TSP are two of the most extensively studied problems in optimization literature. The computational complexity of these problems increases exponentially with the number of destinations or customers. Classical (non-quantum) TSP and VRP algorithms have been used with a measure of success, but there are fundamental limits on what they can achieve.
When Classical Computers Fall Short
For a realistic number of destinations that must be visited, finding the optimal route becomes difficult very quickly. In fact, the size of the search space (the number of possible routes) grows factorially with the number of destinations.
As an example, consider the simpler type of problem, the TSP. If the salesperson has, say, 40 destinations, there are roughly 1047 possible routes that may be taken (see Figure 1). Assume a classical supercomputer is used that can check 1018 combinations per second–which is impressive.
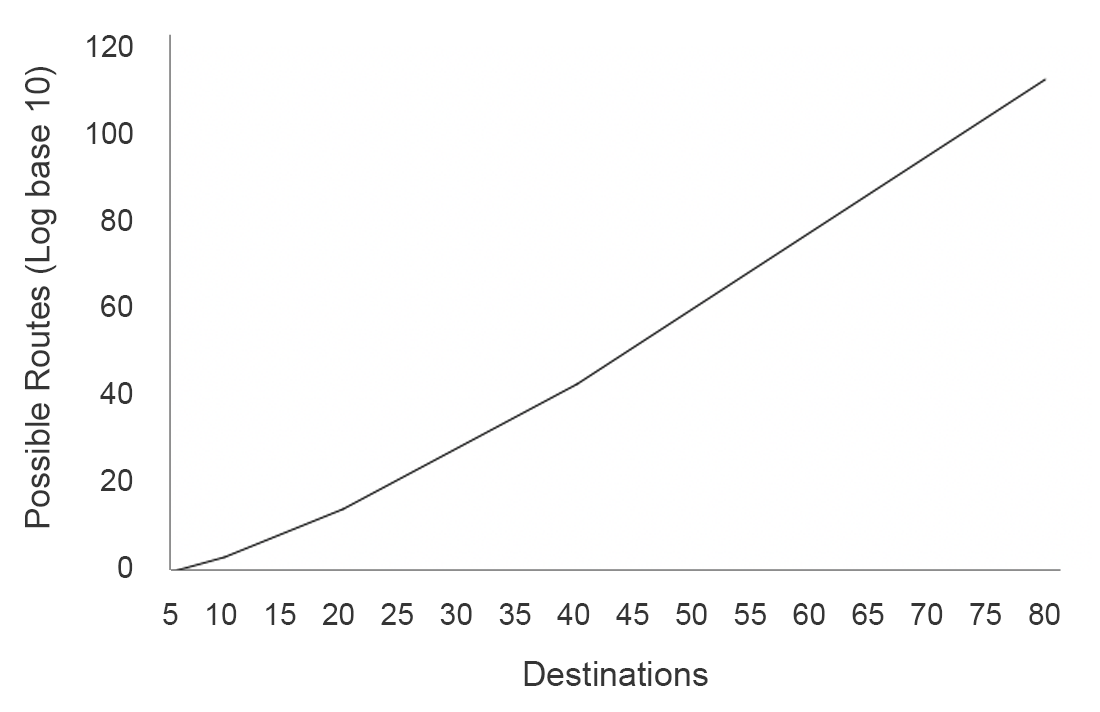
Figure 1: Number of possible routes (in base 10 logarithm) for the TSP given the number of destinations. In other words, the number on the y-axis represents the exponent that 10 must be raised to in order to account for all the possible routes.
It would still take over 1020 (100 billion billion) years of running the supercomputer non-stop for it to brute-force check all possible routes. That is almost 1010 (10 billion) times the age of the universe! Never mind trying to extend this to the VRP where multiple routes must be taken into consideration simultaneously.
This example illustrates how classical computers may run into insurmountable obstacles quickly unless the problems are circumvented by clever algorithms and complex parallel computing techniques. Even so, real-world route optimization problems have an increasing number of constraints to consider, and the problem becomes more complex. Quantum computing is promising for route optimization1–3, why is that so?
Why is Quantum Computing Beneficial for Route Optimization?
Route optimization and other combinatorial optimization problems are naturally well-suited to be solved by quantum computing. In quantum computing, quantum bits, also called qubits, are subject to quantum effects, like superposition and entanglement which can lead to more efficient optimization solutions.
Quantum algorithms work by manipulating qubits using quantum gates (logical operations). These algorithms are carefully designed to maximize the probability of the output qubits containing the optimal result at the end of the computation.
Recently, researchers have shown that it is possible to solve route optimization problems using specialized quantum devices known as quantum annealers. In quantum annealing, the problem is mapped into a form that can be encoded onto qubits, and it is evolved (annealed) slowly to the optimal (or near-optimal) state under the influence of an applied magnetic field.
At the end of the calculation, a quantum annealer outputs a distribution of answers with different probabilities. In order to obtain results with a high degree of confidence, multiple runs have to be performed. Despite this, the total time required for a solution with quantum computing techniques can still be much shorter than with classical algorithms.
Many logistical problems fall under the category of route optimization, touching many aspects of human life, including traffic flow and city infrastructure, ridesharing, navigation, shipping and delivery services, manufacturing tasks, and scheduling, just to name a few.
As the demands of these services continue to expand in scale and complexity, quantum and quantum-inspired computing can be the answer to solving logistical problems more efficiently.
Check our Research page for an upcoming research paper on applying quantum annealing to the VRP.
Subscribe to the 1QBit Blog to keep up with many other topics in advanced and quantum computing.
References
1 S. Feld, C. Roch, T. Gabor, C. Seidel, F. Neukart, Galter Isabella, W. Mauerer, C. Linnhoff-Popien, “A Hybrid Solution Method for the Capacitated Vehicle Routing Problem Using a Quantum Annealer”, Frontiers in ICT, 6(13), DOI: 10.3389/fict.2019.00013 (2019)2 J. Clark, T. West, J. Zammit, X. Guo, L. Mason, and D. Russell, “Towards Real Time Multi-robot Routing using Quantum Computing Technologies”, In Proceedings of the International Conference on High Performance Computing in Asia-Pacific Region, Association for Computing Machinery, New York, NY, USA, 111–119 DOI:https://doi.org/10.1145/3293320.3293333 (2019).
3 H. Irie, G. Wongpaisarnsin., M. Terabe, A. Miki, S. Taguchi, “Quantum Annealing of Vehicle Routing Problem with Time, State and Capacity”, Quantum Technology and Optimization Problems, Lecture Notes in Computer Science, 11413, (2019).