Computing comes down to harnessing physics in different ways in order to process information. The difference between classical computing and quantum computing is in manipulating bits versus quantum bits, also called qubits. Much like bits, the two levels of a qubit are labelled by 0 and 1. Examples of qubits include electron spin or the polarization of light. What are electron spin and light polarization?
Spin is a quantum property of particles and can be thought of as an intrinsic angular momentum. Electron spin is what governs, for example, how otherwise identical electrons occupy energy levels around the nucleus of an atom, and why they do not all occupy the same energy level. That is why spin is partly responsible for why atoms are organized the way they are on the periodic table of the elements. Here, the point about spin is that electrons can either be in a spin-up or spin-down state or a superposition thereof: These two different spin states define a two-level system that can be used as a type of qubit.
Quantum superposition allows for an exponentially growing amount of information that can be manipulated by quantum algorithms.
Polarization is the direction of the oscillation of light. An example is linear polarization, where light either oscillates up-down (vertically) or side-to-side (horizontally). In this case, vertical and horizontal polarizations could also be used to define the two levels of a qubit.
The above two examples are among the many ways a qubit can be physically implemented. Regardless of how a qubit is made, one of the levels is called 0, and the other is called 1. A key feature of qubits is that they can exist in any combination of both levels—known as quantum superposition. Note that this is not some magic fact that allows for quantum computers to spit out many results simultaneously: The output of a qubit will always either be 0 or 1, the same as a bit.
Think of a Globe
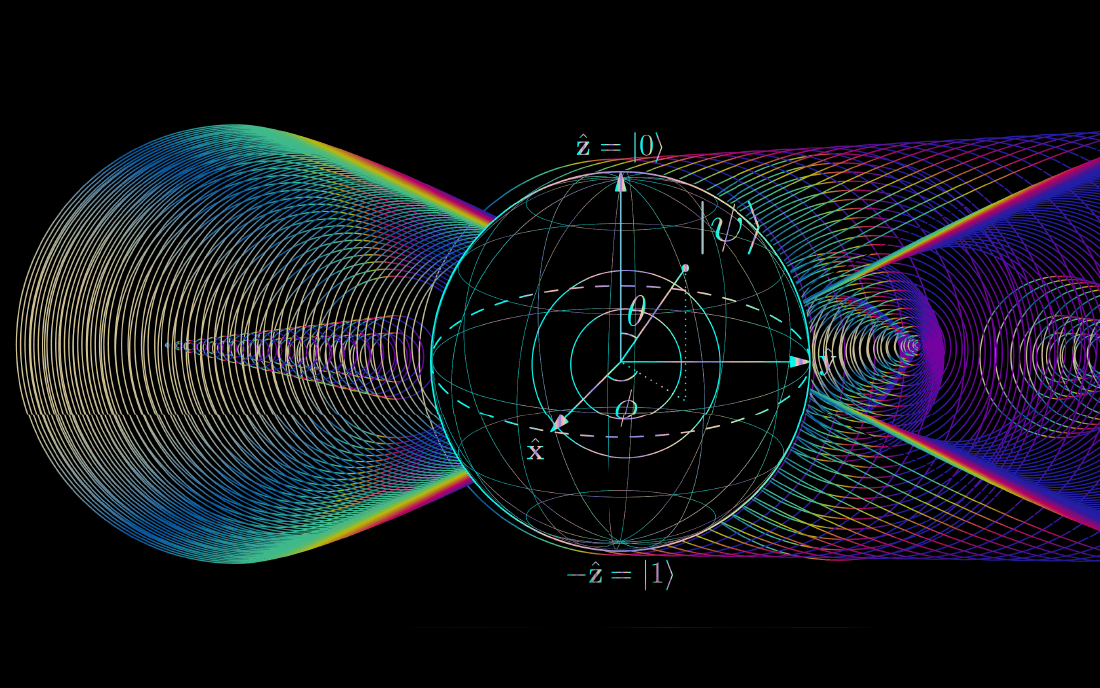
To understand what is really going on with qubits and how they differ from bits, it helps to picture a globe, as in Figure 1 below. In this analogy, bits only exist at either pole. On the other hand, a qubit can exist at any point on the surface of the globe. The particular mixture of 0 and 1 specifies the exact location. Quantum algorithms can use quantum gates which are operations that move the qubit state around the surface of the globe to perform computations. Quantum algorithms will be discussed further in an upcoming article.
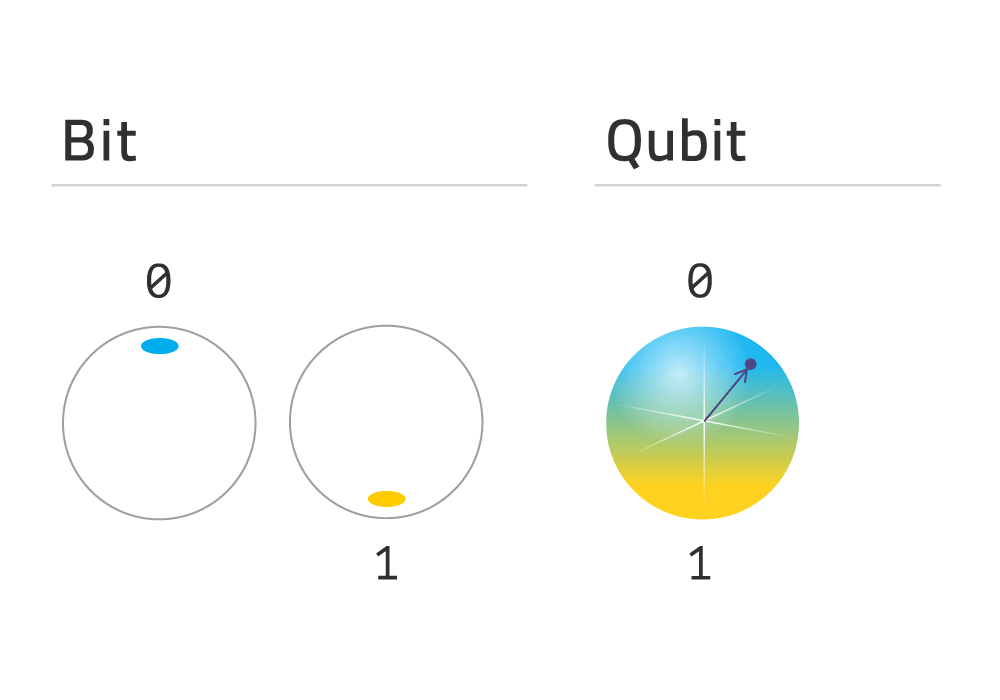
Figure 1: Visualizing a bit and a qubit.
When a qubit is measured along its vertical axis, it ‘collapses’ to either 0 or 1 with certain probabilities—a fundamental feature of quantum measurements. In the image above, the qubit state (the point indicated by the black arrow) is in the northern hemisphere so it will probably collapse to 0 (the north pole). The closer the qubit is to a pole, the more likely it is to settle there upon measurement.
So, What Is the Point?
While it is interesting that a single qubit can represent a combination of both 0 and 1 states, it is instructive to consider more than one qubit to understand the potential advantage of using qubits.
For two qubits, we need four states (and their combination) to describe the superposition state. As an example, consider the case of electron spin qubits depicted in Figure 2 below.
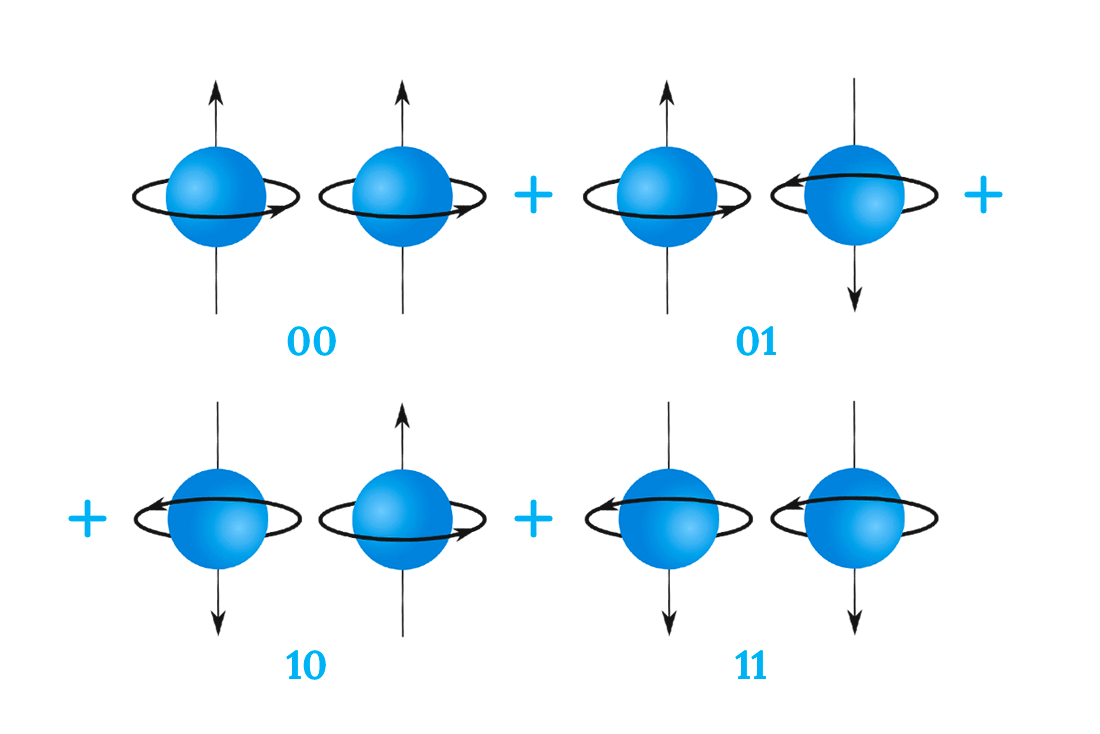
Figure 2: A superposition of the four states of two electron spin qubits: 1st electron is spin up, 2nd is spin up (00 state) + 1st electron is spin up, 2nd is spin down (01 state) + 1st electron is spin down, 2nd is spin up (10 state) + 1st electron is spin down, 2nd is spin down (11 state).
The number of states needed to describe the multi-qubit system increases exponentially with the number of qubits. For two qubits, we need four states; for three qubits, eight states, and so forth.
The point: quantum superposition allows for an exponentially growing amount of information that can be manipulated by quantum algorithms. A challenge is to make sure all the information is manipulated in the right way; the more qubits that are used in a computation, the more challenging it is to ensure that a desired outcome is achieved.
It is also a challenge to make sure that quantum computations are not overtaken by errors which is a difficult task since qubits are highly sensitive to their external environments and can lose their information easily.
There is more to the story of quantum computing. Crucial to creating useful quantum algorithms and performing quantum error correction is quantum entanglement, a different feature of quantum mechanics where particles are linked together in a shared quantum state, regardless of how far apart they are.
Subscribe to the 1QBit blog below to learn more about harnessing quantum physics in computation, including quantum entanglement, quantum algorithms, and more.
We respect your privacy. If you subscribe, we will never spam you or sell, rent, lease, or give away your information to any third party.