Artificial intelligence is set to become a $126.0B industry by 2025.¹ Machine learning is a major part of artificial intelligence involving algorithms that improve in performance over time given more data. Applications of machine learning include image and speech recognition, assisted medical diagnoses, traffic prediction, self-driving cars, and stock market trading. New applications are springing up all the time as society becomes more complex. However, the rapid growth in the amount of available real-world data requires increasingly faster classical computers (“classical” meaning not quantum). These computers are limited because the computational resources quickly become unreasonable for machine learning for large, complex datasets.
“Quantum information processing is likely to have a far-reaching impact in the field of machine learning and artificial intelligence as a whole.”
Using quantum computers to enhance machine learning is a promising approach to handle problems involving big data. Quantum computing is likely to have a far-reaching impact in the field of artificial intelligence. This is because quantum algorithms are, in theory, faster at solving some problems compared to classical computers. When quantum computers have become more developed, they may even solve problems that are impossible for classical computers.
The Random Kitchen Sinks Method
Even though they are still in the early stages of development, current quantum computers provide a platform for studying whether there is a quantum advantage for machine learning. One study was explored in a recently published 1QBit paper.² A classical machine learning algorithm called “random kitchen sinks”³ (RKS) was improved using a quantum–classical hybrid approach.
The RKS algorithm can be used to solve a common problem in machine learning known as classification. The goal is to train an algorithm so it can make accurate classifications of the features in the data by taking enough random samples, short of using the proverbial “kitchen sink”. A feature is a property of the dataset you are interested in, such as the colours orange and green shown in Figure 1.
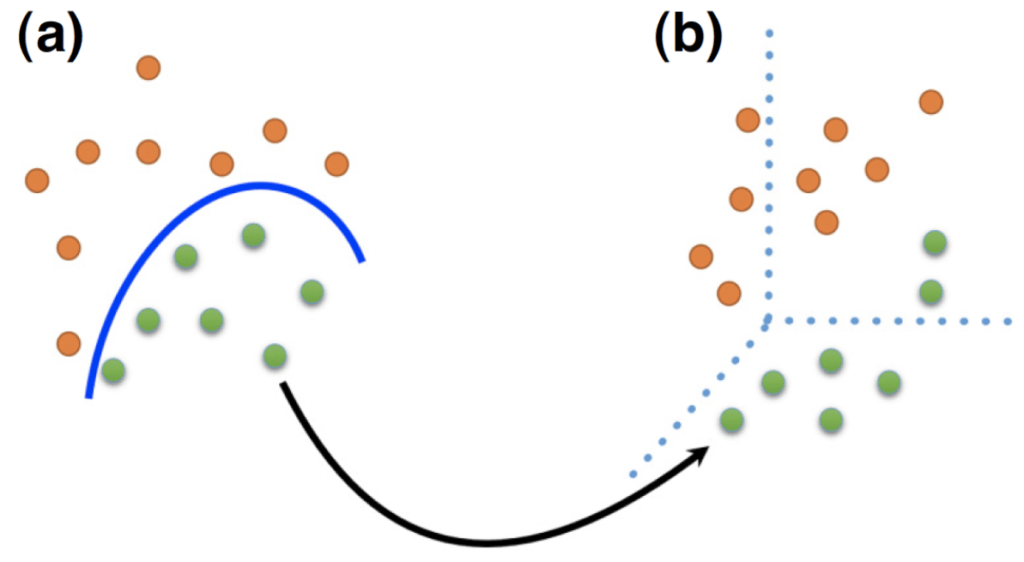
Figure 1: A classification problem where the goal is to train the algorithm to distinguish two classes of orange- and green- coloured data samples. Each data sample in (a) is mapped into the new space in (b) to systematically make the classification.
Choosing features at random reduces the initial tweaking that must be done in the classification task, reducing the computational overhead. As a simple analogy, it is like playing a game of Twenty Questions. Here, though, instead of always asking well-designed questions, you ask random questions in order to accomplish your classification task. If enough random questions are asked, a meaningful result can be obtained. The RKS algorithm provides a simple way to generate accurate learning algorithms that run fast and are easy to implement.
How is quantum computation used to improve RKS?
Analog quantum computation is one of the main branches of quantum information processing. The idea is to encode your problem as a quantum system by relating the parameters in your task to parameters of the quantum model. The system is then changed by using an applied magnetic field. If the system is changed slowly enough, the end result can be a system that corresponds to the solution of your problem.
In the mentioned work,² RKS is enhanced with analog quantum computation. The difference is in how the random selection is done. Here, the random features are obtained by mapping the problem into a quantum problem as described in the previous paragraph, and then choosing the random features. This results in quantum randomization.
How does it compare to the classical approach?
The authors demonstrated how effective their algorithm is on both a synthetic dataset and a real-world dataset to be able to study both ideal and real-world types of problems. They solved each problem with and without quantum randomization and compared the results.
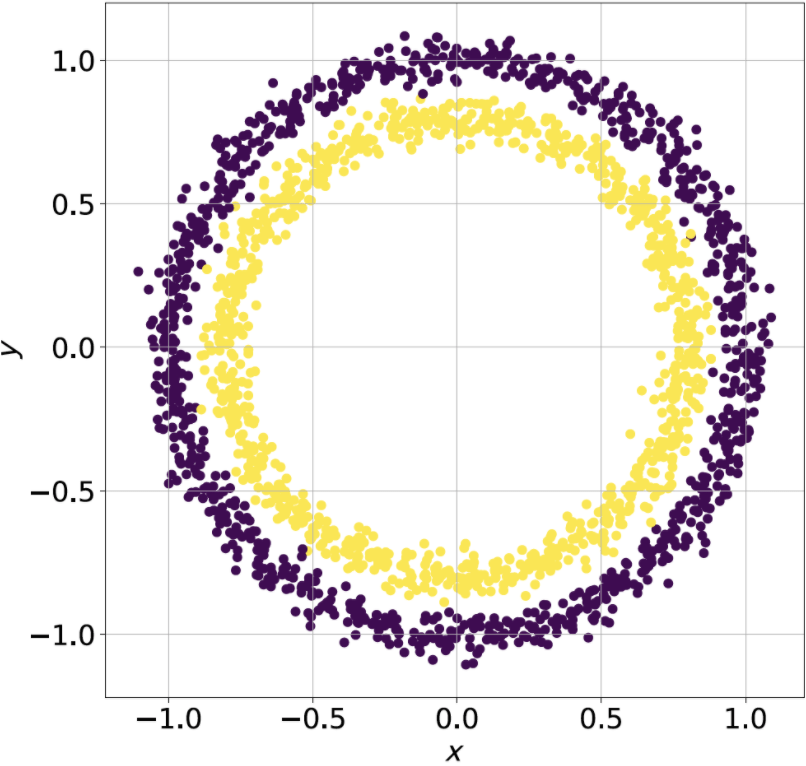
Figure 2: Representation of the synthetic “circles” dataset. There are two classes (yellow and purple), based on an arbitrary radius consisting of 1000 data samples each.
For the synthetic dataset (see Figure 2), classification accuracy without quantum randomization is at most 50%. The quantum algorithm was able to achieve an impressive 99.4% accuracy.
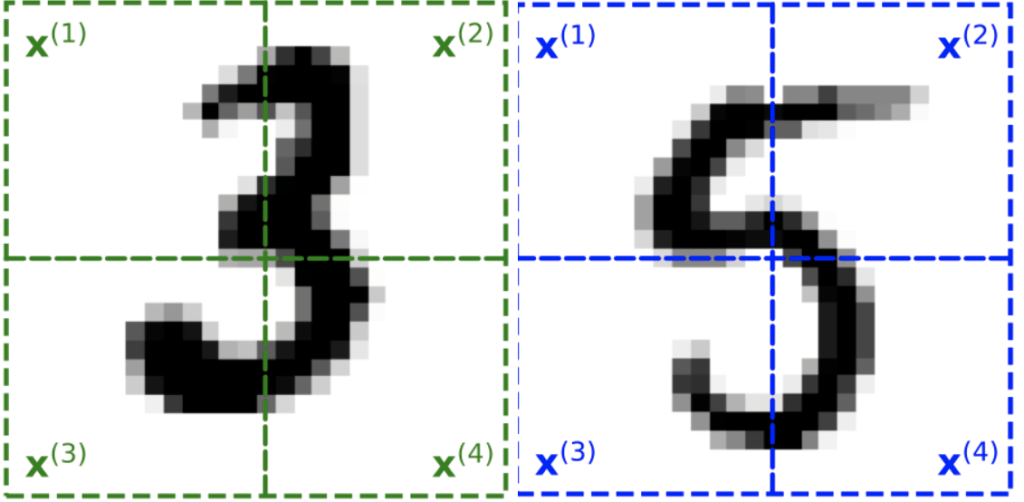
Figure 3: Samples of the digits “3” and “5” from the MNIST dataset. Four qubits are used to encode each quarter of the image into a quantum system.
For the real-world dataset (see Figure 3), the task of classifying samples of the digits “3” and “5” from the popularly used MNIST dataset was studied. The classification accuracy without quantum randomization was 95.6%. The quantum algorithm was able to achieve 98.4% accuracy.
The authors note that there are classical methods that can perform as well as, or slightly better than, the quantum algorithm for the dataset studied. However, such methods require more computing resources, which can become problematic with big datasets. Also, the authors note that the performance of the quantum algorithm could be improved by tweaking its parameters.
Conclusion
The above work² points to the promising potential of quantum-enhanced machine learning, especially as real-world data becomes more complex and more sophisticated quantum hardware is developed. Quantum information processing is likely to have a far-reaching impact in the field of machine learning and artificial intelligence as a whole.
Even now, there is the potential to attain a quantum advantage through hybrid quantum–classical machine learning algorithms. The proposed quantum algorithm presents the possibility of using current quantum devices for solving practical machine learning problems.
For more information on how quantum computing can enhance classical computing, subscribe to the 1QBit blog.
References
¹ L. Columbus, “Roundup Of Machine Learning Forecasts And Market Estimates”, Forbes (2020).
² M. Noori, S. S. Vedaie, I. Singh, D. Crawford, J. S. Oberoi, B. C. Sanders, and E. Zahedinejad, “Analog-Quantum Feature Mapping for Machine-Learning Applications”, Phys. Rev. Appl. 14, 034034 (2020).
³ A. Rahimi and B. Recht, “Weighted sums of random kitchen sinks: replacing minimization with randomization in learning”, NIPS08: Proceedings of the 21st International Conference on Neural Information Processing Systems, 1313–1320 (2008).