Many problems in finance take the form of mathematical optimization problems. As an example from portfolio optimization, an asset manager may be tasked with allocating funds across a pool of assets while maximizing the return at a given level of risk. However, conventional approaches often fail when computational resources cannot handle the amount of “noisy” real-world data (i.e., useful data that is corrupted or distorted by other, meaningless data), or extrapolating for missing data, or account for the correlations between all assets.
It is promising to note that as the fields of advanced and quantum computing mature, quantum devices will increasingly be used to tackle problems that would be challenging, or even impossible, for classical (non-quantum) computers to handle. Yet, even now advanced and quantum computing methods have demonstrated impressive results with respect to the application of quantum-inspired optimization algorithms to financial problems.
In this article, two examples are discussed that highlight how framing financial problems as what are known as “quadratic unconstrained binary optimization” (QUBO) problems1 might allow for more-efficient solutions to financial problems that contain risk, leading to safer investments. QUBO problems are specially formulated for being solved using quantum annealers,2, 3 but can be solved using classical solvers or gate model quantum devices.
The general consensus among quantum hardware researchers is that attention has largely shifted from quantum annealers to gate model quantum computers. However, the issue is still open, especially for native QUBO problems, which may be especially suited to be solved using quantum annealers. Two such problems are the long–short risk parity problem and the optimal feature selection problem, discussed below. In addition, the related “quantum-inspired hierarchical risk parity” (QHRP) problem is covered, which is not a native QUBO problem but also shows promising results in its potential to be solved using a quantum annealer.

Application #1: Improving Risk Parity Methods
Risk parity is an approach to investment portfolio optimization where assets are weighted differently according to their risk. A number of efficient algorithms exist to solve risk parity optimization problems. These methods can provide elegant mathematical solutions to such problems in the academic world of perfectly estimated risks and returns, but they fail to capture important practical considerations. For real-world data, they can yield instability in the results or omit vital information, such as how certain assets are related to one another. What can be done in light of these issues?
The hierarchical risk parity (HRP) method4 is designed to address these shortcomings. The motivation behind HRP is that assets have a hierarchical structure; for example, stocks behave differently than bonds, and stocks of small pharmaceutical companies behave differently than stocks of large public utility companies. Therefore, grouping the assets in a hierarchical way is more efficient than attempting a simultaneous brute-force optimization of all assets.
As an example,5 Fig. 1 depicts a hierarchical clustering tree with data from a commodity trading advisor (CTA) portfolio, with the set of all pertinent assets as the root, and the leaves consisting of all of the assets in their own clusters.
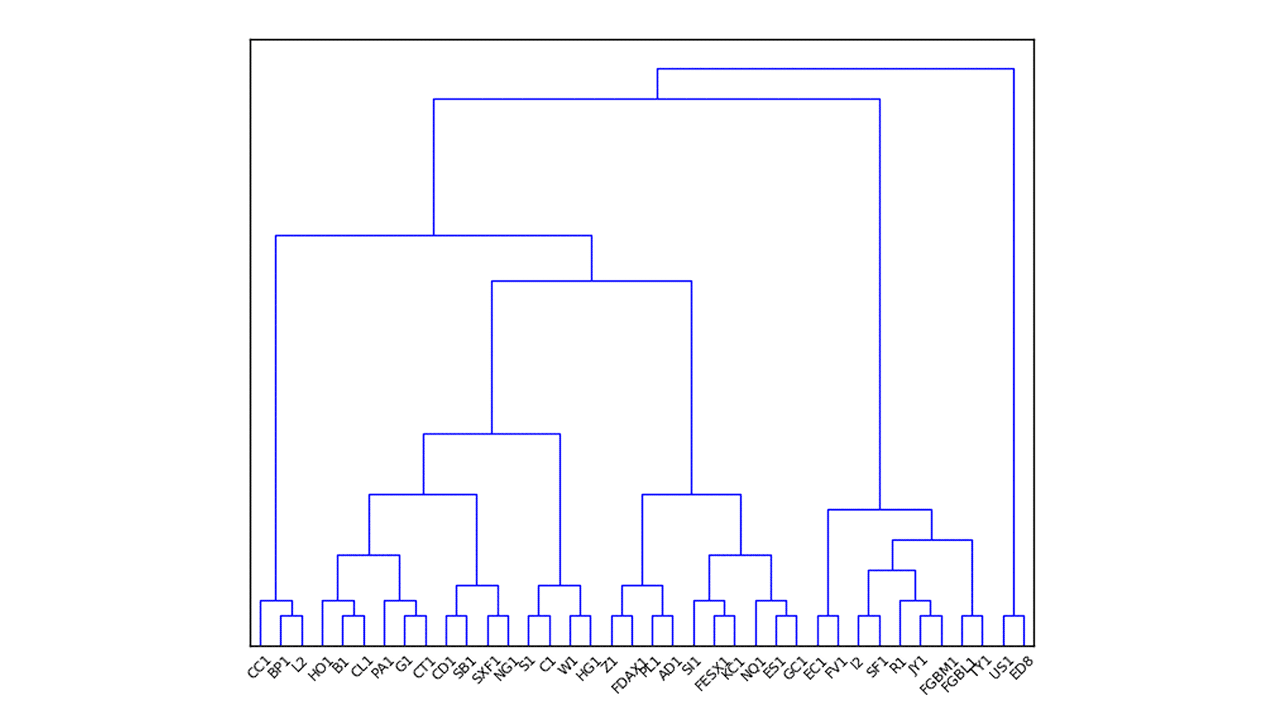
Figure 1: Example hierarchical clustering tree from 2014 for the CTA dataset.
The HRP algorithm is effective because it solves simple, two-asset optimization problems many times instead of solving a single large, many-asset problem.
While HRP is already an improved optimization method, it is possible for QHRP to outperform standard HRP and other conventional methods with respect to minimizing risk.5 The crux of this new approach lies in framing the problem in QUBO form, as well as choosing a different way to cluster the assets. QHRP problems may be solved with quantum annealing techniques using either quantum or classical hardware. For now, classical hardware is better-suited for such problems, as the number of fully connected qubits on current quantum hardware is still modest. However, the solution potential for quantum hardware is deep. For instance, the complexity of the QUBO problem that can be solved grows with the number of available fully connected qubits. Eventually, the solution potential on quantum hardware should supersede that of classical hardware.
Results show that it is possible for QHRP to outperform alternative methods, including standard HRP, for a variety of risk measures.5 In the referenced work, the annualized volatilities of portfolio returns for QHRP were on average 16% lower than the annualized volatilities present when using standard HRP.
Many risk parity strategies dictate long-only positions, meaning that the investor has bought and owns shares of assets with the expectation that they will increase in value in the long term. It has been shown that a more robust method would be to allow for both long and short positions (long–short optimization), resulting in more degrees of freedom for risk parity portfolio optimization.6 By weighting the assets according to their risk and allowing for both long and short positions, the problem can again be framed in a way suitable for quantum annealing, similarly to the above method, allowing for the solution to be run on either a quantum or classical computer.
Results6 have shown that the method of long–short optimization using quantum annealing is not as sensitive to large maximum drawdowns, meaning, for example, that this investment optimization strategy is resilient to financial crises. Higher risk-adjusted returns were also achieved compared to other methods.
Application #2: Quantum Annealing and Optimal Feature Selection in Credit Scoring
The goal of credit scoring is to quantify how reliable a borrower looks to potential lenders. A credit score is a numerical expression based on an analysis of different features of the applicant—their chequing and savings accounts, payment history, level of debt, and loans from other institutions, among other factors. The higher the credit score, the better an applicant may look to potential lenders.
Feature selection is motivated by the intuitive concept that not all features are equally important. To provide an example,7 in Fig. 2, the feature variables from the German Credit Data from UC Irvine are ranked by their Spearman correlation coefficient (numerical correlation measure) with the classification variable given as a measure of how relevant each feature is for the purposes of credit scoring.
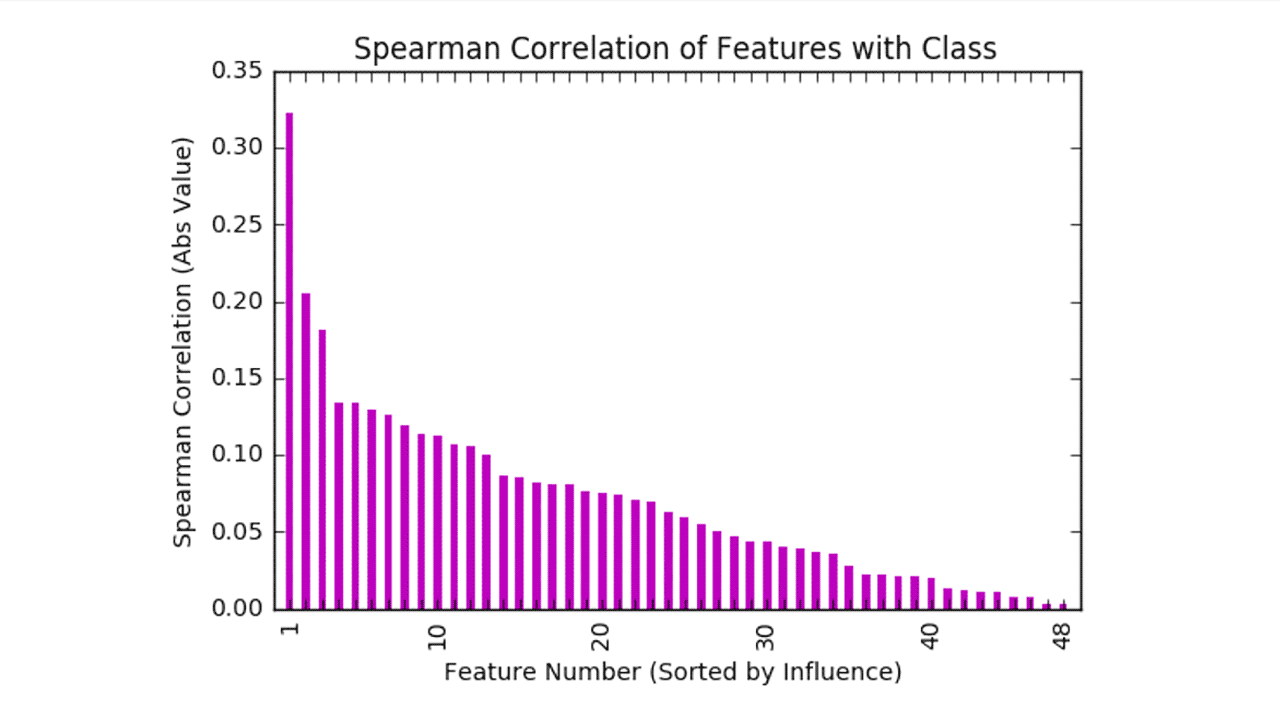
Figure 2: Spearman correlation. The most influential features involve the status of the applicant’s chequing account, savings account, and loans at other institutions, all of which are included in all practical feature subsets. As we move towards the right, however, the influence of each new feature declines.
Therefore, with feature selection—selecting the most relevant features in a given dataset—one can reduce the number of variables input to an algorithm known as a classifier. This can be done using a QUBO model, which attempts to select features that are both independent and influential. A credit scoring problem scales exponentially with the number of features, meaning that it quickly becomes intractable using classical techniques when attempting to take into account a more realistic (i.e., real-world) number of features.
Tests were conducted using the German Credit Data, and the results were compared with those reported in the literature.7 In comparison with other techniques, QUBO feature selection yielded a smaller feature subset with no loss of accuracy, opening up the possibility of using quantum annealing to reduce the size of very large feature sets, especially as quantum hardware matures. It was also found that using different correlation methods could result in an improvement in performance.
Summary
Applying optimization techniques from advanced and quantum computing can result in reduced risk and can handle financial optimization problems more efficiently without a loss of accuracy. Further study is needed to explore additional merits of such quantum-inspired methods within the vast parameter space of asset optimization problems. As such methods are developed, and as quantum hardware continues to improve, solution accuracy and potential should continue to increase. This could open the door to further and greater applications in business and finance.
Even today, you can use QHRP methods to optimize your financial portfolio with 1QBit’s cloud service, 1Qloud.
References
1 F. Glover, G. Kochenberger, and Y. Du, “A Tutorial on Formulating and Using QUBO Models”, arXiv:1811.11538, (2019).
2 M. W. Johnson, M. H. S. Amin, S. Gildert, T. Lanting, F. Hamze, N. Dickson, R. Harris, A. J. Berkley, J. Johansson, P. Bunyk, E. M. Chapple, C. Enderud, J. P. Hilton, K. Karimi, E. Ladizinsky, N. Ladizinsky, T. Oh, I. Perminov, C. Rich, M. C. Thom, E. Tolkacheva, C. J. S. Truncik, S. Uchaikin, J. Wang, B. Wilson, and G. Rose, “Quantum annealing with manufactured spins”, Nature, 473, 194–198 (2011).
3 1QBit, “From Chemistry to Finance: The Broad Scope of New Quantum Optimization Methods”, (2020).
4 M. López de Prado, “Building Diversified Portfolios that Outperform Out of Sample”, Journal of Portfolio Management, (2016).
5 E. Alipour, C. Adolphs, A. Zaribafiyan, and M. Rounds, “Quantum-Inspired Hierarchical Risk Parity”, (2016).
6 G. Rosenberg and M. Rounds, “Long-Short Minimum Risk Parity Optimization Using a Quantum or Digital Annealer”, (2018).
7 A. Milne, M. Rounds, and P. Goddard, “Optimal Feature Selection in Credit Scoring and Classification Using a Quantum Annealer”, (2017).